- Published on
Beginners guide to building boolean expression compiler
- Authors

- Name
- Samarjit Samanta
- @samarjitsamanta
This is a two part series. This is part 1, where we will learn to create a boolean expression parser which will read the expression and convert into a abstract syntax tree. The second part is using that syntax tree and evaluate on a context object. The context is shopping cart and we will define a promotion as a boolean expression.
We will begin by defining the grammar in pegjs. PEG.js is a parser generator for javascript. Our expression will be a boolean expression. It can have function calls. Lets assume this expression works on a javascript object.
context = {
name: 'sam',
address: {
addressLine: '2400 Dallas Pkwy',
apartment: '356',
state: 'TX'
},
projects: [
{ projName: 'pegjs parser', year: 2019 },
{ projName: 'pratt parser', year: 2019 },
{ projName: 'MyIMX233 PCB', year: 2017 }
],
blogs: [
{ title: 'naive react', year: 2019 },
{ title: 'naive redux', year: 2018 }
]
}
Lets target these rules
These rules take the context and can evaluate to some boolean result. These are mostly like filters, we can call these kinds of expressions as predicates. Then these predicates can be grouped into parenthesis. Also there can be functions calls which may return a number or boolean. If these return number we do some math on the result whose result will be boolean. Then comes the argument of functions. The arguments take the array name as first parameter, and a predicate as second parameter.
`name='sam' and address.addressLine='2400 Dallas Pkwy'`
`name='sam' and count('projects', year=2019) > 1`
`name='sam' and (exists('projects') or exists('blogs'))`
`name='XX' and (address.state='TX' or address.state='CA')`
`name='XX' and address.state='TX' and address.apartment=356`
Grammar
In this whole article I will try to built the grammar and output will be AST (abstract syntax tree). The actual evaluation of AST might be part of another blog. So we are mostly working on the parser part of it. The generator is responsible of reading the AST and producing a target language syntax (ex. js, java) or object code.
This blog might get rather long, since I am going to show all steps and intermediate results. So that you get the hang of thinking process.
Other approaches
Another approach of parsing these expressions would be to use a hand written parser. A decent one can be written using recursive descent or pratt parser.
Simple Predicate
It has only one line basically left hand side+operator+right hand side. The lexer regex’es are one single terms. These are combined to create larger expressions. Lets parse this expression address.state='TX'.

Expression term
start = Predicate
Predicate = left:identifier op:op right:value {return {op: op, left, value: right};}// lexer regex
op = '='value = _ id:[a-zA-Z0-9'-]+ _ {
return id.join('');
}
identifier = _ id:[a-zA-Z\.]+ _ {
return { name: id.join(''), type: 'identifier' };
}integer "integer"
= _ [0-9]+ { return parseInt(text(), 10); }_ "whitespace"
= [ \t\n\r]*
Simple Predicate Output
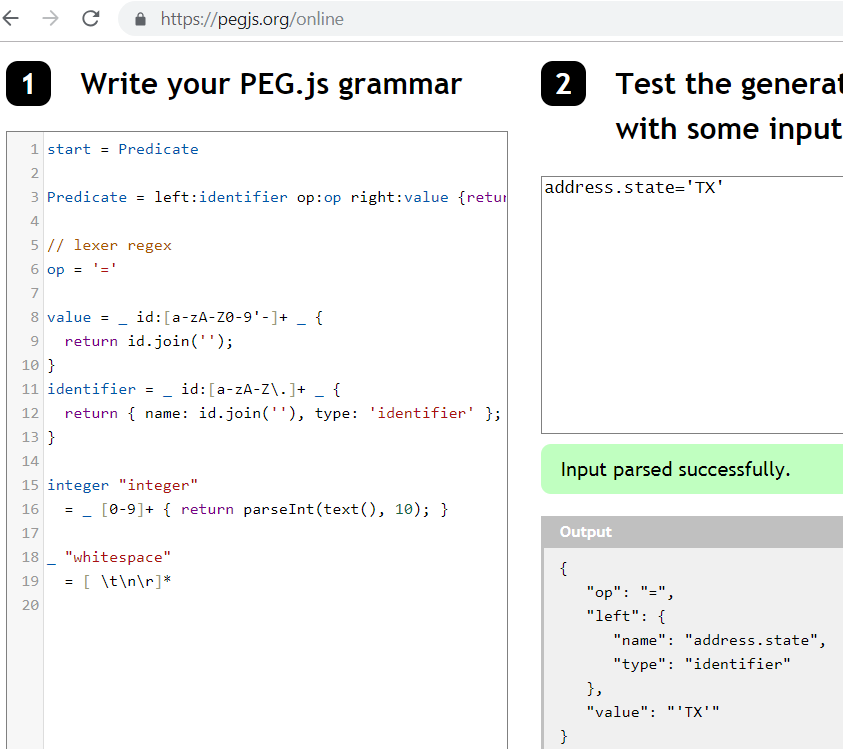
Output for address.state='TX'
Extrapolating this technique can deal with binary operator expressions like this name='XX' and address.state='TX'. But how can we chain these expressions. Lets target name='XX' and address.state='TX' and address.apartment=356 next. We need to still make our expression backward compatible. Like if only name='XX' is there without any and, it should still work. The little /Predicate does the trick. It tells AndExpr if it does not find the head or tail then fallback to match only Predicate.
start = AndExpr
AndExpr = head:Predicate tail:('and' Predicate)+ {
let accum = [head];
tail.reduce((accumulated, element) => {
accumulated.push(element[1]);
return accumulated;
}, accum);
return {op: 'and', predicates: accum};
}
/PredicatePredicate = left:identifier op:op right:value {return {op: op, left, value: right};}
Output
{
"op": "and",
"predicates": [
{
"op": "=",
"left": {
"name": "name",
"type": "identifier"
},
"value": "'XX'"
},
{
"op": "=",
"left": {
"name": "address.state",
"type": "identifier"
},
"value": "'TX'"
},
{
"op": "=",
"left": {
"name": "address.apartment",
"type": "identifier"
},
"value": "356"
}
]
}
Dealing with parenthesis should not be much of a problem. But sometimes recursion will take a while to wrap your head around this.
start = OrExpr
OrExpr = head:AndExpr tail:(_ 'or' _ AndExpr)+ {
let accum = [head];
tail.reduce((accumulated, element) => {
accumulated.push(element[3]);
return accumulated;
}, accum);
return {op: 'or', predicates: accum};
}
/AndExpr
AndExpr = head:ParenExpr tail:(_ 'and' _ ParenExpr)+ {
let accum = [head];
tail.reduce((accumulated, element) => {
accumulated.push(element[3]);
return accumulated;
}, accum);
return {op: 'and', predicates: accum};
}
/ParenExprParenExpr = "(" exp:AndExpr ")" { return exp; } / Predicate
At this point we are able to handle this kind of expressions name=’XX’ and (address.state=’TX’ and address.apartment=356) and y=10
Lets get the call expressions working. There is quite a bit going on here to disambiguate between and(...) vs fn(...). Note the keyword and. To get around this we have to use ReservedWords concept. Since andis a reserved word, it will not match the CallEx. Notice how ArgsExpr also contains the OrExpr. Then finally the call function may be part of left hand side of an expression.
start = OrExpr
...
AndExpr = head:CallExpr tail:(_ 'and' _ CallExpr)+ {
let accum = [head];
tail.reduce((accumulated, element) => {
accumulated.push(element[3]);
return accumulated;
}, accum);
return {op: 'and', predicates: accum};
}
/CallExprCallExpr = callex:CallEx _ op:op _ val:value { // functionRet() > 0
return {op, callex, value: val};
}
/CallExArgsExpr = head:value _ ',' _ tail:OrExpr {
tail.path = head;
return tail;
}
/value
CallEx = !ReservedWord ident:[a-zA-Z]+ '(' _ args: ArgsExpr _ ')' { // functionThatReturnsBoolean()
return {type: 'CalExpr', name: ident.join(''), args: args};
}
/ ParenExpr
ParenExpr = "(" exp:AndExpr ")" { return exp; } / Predicate...
This is already capable of parsing name=’XX’ and count(‘blog’, address.state=’TX’ and address.apartment=356) > 0 and y=10.
Full Implementation showing all the use cases
I did modify a bit, like the value expression now understands quoted string and the terminating quote should be same as starting quote, still it can be improved to understand escape sequence. Also spaces are included as part of value since we have quoted string.
Below you can see all the expressions in action.
All use cases + live expression evaluation with errors
Conclusion
Now we have got a working lexer parser using pegjs grammar which produces AST. Writing this parser coding by hand would have taken a lot more thought process, but we could get a faster performance. Feel free to write a generator to execute these rules against the actual json context we imagined in the beginning. I will share the link in this post if you post in comments.
Second part is all about evaluate the abstract syntax tree that we created in this part of the tutorial